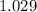Answer:
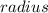 ≈
≈
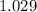
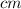
Explanation:
Knowing that the formula for the volume of a sphere is:
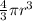
We can set the equation equal to 4.57.
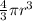
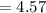
We divide both sides by
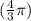 so we can get
so we can get
 by itself.
by itself.
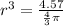
We simplify and get:
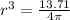
Taking the cube root of both sides, we then get the radius:
![r=\sqrt[3]{(13.71)/(4\pi ) }](https://img.qammunity.org/2023/formulas/mathematics/high-school/z5m4dn8y9zbhp5zv8o0a2npnfr7u8ho56j.png)
The approximate answer comes out to be:
 ≈
≈