Question

Question is in photo,

Answer 1

The partial derivatives of the function given are, respectively:
`f_(x) (x, y) = - 3 \cdot x^2 + y^4`,
`f_(y)(x, y) = 4\cdot x\cdot y^(3) + 36\cdot y^(5)`.

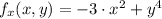How to find partial derivatives of a multivariate function

In this problem we find the case of a function with two variables (x, y), whose partial derivatives must be found. The procedure is now shown:

1. Choose the variable to be differentiated.
2. Assume that the remaining variables are constants.
3. Use derivative rules.
4. Write the resulting expression.

Now we proceed to determine all partial derivatives:

Choose the variable to be differentiated: x.

Variable assumed to be constant: y.

Use derivative rules and write the resulting expression:

`f_(x) (x, y) = - 3 \cdot x^2 + y^4`

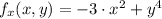
Choose the variable to be differentiated: y.

Variable assumed to be constant: x.

Use derivative rules and write the resulting expression:

`f_(y)(x, y) = 4\cdot x\cdot y^(3) + 36\cdot y^(5)`