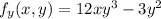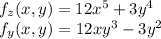
The given function is f(x, y) =
 . To find the partial derivatives of f, we treat y as a constant when taking the partial derivative with respect to x, and vice versa.
. To find the partial derivatives of f, we treat y as a constant when taking the partial derivative with respect to x, and vice versa.
Finding
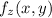
When taking the partial derivative with respect to x, we treat y as a constant. Therefore, the partial derivative of f with respect to x is:
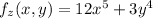
Finding
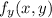
When taking the partial derivative with respect to y, we treat x as a constant. Therefore, the partial derivative of f with respect to y is: