Question

Write the exponential function y=4(1.28)^t in the form y=ae^kt.

(a) Once you have rewritten the formula, give accurate to at least four decimal places.
help (numbers)

If is measured in years, indicate whether the exponential function is growing or decaying and find the annual and continuous growth/decay rates. The rates you determine should be positive in the case of growth or decay (by choosing decay the negative rate is implied).

(b) The annual rate is % per year (round to the nearest 0.01%).

(c) The continuous rate is % per year (round to the nearest 0.01%).

Answer 1

a. The rewritten exponential function is k = 0.263

b. The annual growth rate is 51.8%

c. The continuous growth rate is 26.3%.

To rewrite the exponential function y =
`4(1.28) ^t` in the form y=a
`e ^(kt)` , we can take the natural logarithm of both sides:

`\ln(y) = \ln(4(1.28)^t)`

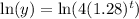
Using the distributive property of logarithms, we can rewrite the right-hand side as follows:

`\ln(y) = \ln(4) + \ln(1.28)^t`

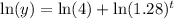
Since
`(1.28) ^t =e^tln(1.28)` , we can substitute this into the equation to get:

`\ln(y) = \ln(4) + t \ln(1.28)`

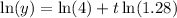
Comparing this equation to the standard form y=a
`e^( kt)`, we see that a=e ln(4) =4 and k=ln(1.28). Therefore, the rewritten equation is:

y = 4
`e^(0.263t)`

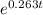
To find the annual growth rate, we can substitute t=1 into the equation and solve for y:

y = 4
`e^(0.263)` = 5.18

This means that the value of y increases by 51.8% each year.

The continuous growth rate is equal to the value of k in the exponential function, which is ln(1.28)=0.263. This means that the value of y increases by 26.3% continuously over time.