Question

Which equation models the line on the graph?

(-1,4)
(3,2)
O A) y-2= -1/2(x-3)
O B) y + 2 = -1/2 (x+3)
O C) y-2=-2(x-3)
OD) y + 2 = -2(x+3)

Answer 1

The equation that models the line passing through the points (-1, 4) and (3, 2) is
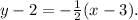`\(y - 2 = -(1)/(2)(x - 3)\).` thus option A is correct.

Step-by-step explanation:

To determine the equation of the line passing through the given points (-1, 4) and (3, 2), we can use the point-slope form of a linear equation, which is
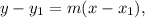`\(y - y_1 = m(x - x_1)\),` where
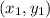`\((x_1, y_1)\)` are the coordinates of a point on the line, and (m) is the slope. The slope (m) can be calculated using the formula
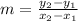`\(m = (y_2 - y_1)/(x_2 - x_1)\)` with the given points (-1, 4) and (3, 2). Substituting these values, we find that
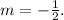`\(m = -(1)/(2)\).` Choosing one of the points, say (-1, 4), we substitute the values into the point-slope form, resulting in the equation
`\(y - 2 = -(1)/(2)(x - 3)\).`

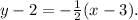
Now, let's check each given option. Option (A) matches the derived equation,
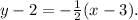`\(y - 2 = -(1)/(2)(x - 3)\).` Options (B), (C), and (D) have different slopes or intercepts, and thus, they do not represent the line passing through the specified points.

In conclusion, the correct equation is (A)
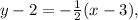`\(y - 2 = -(1)/(2)(x - 3)\),` as it accurately models the line passing through the given points (-1, 4) and (3, 2).