Question

A) Show that the equation 20-x^3-7x^2=0 can be rearranged to give x=20/x^2 - 7

b) using xn+1 = 20/x^2 - 7 with x0 = -9 find the values of x1, x2 and x3
C) explain what the values of x1, x2 and x3 represent

Answer 1

(a) Proof below.

`\begin{aligned}\textsf{(b)} \quad x_1&=-6.75308642\\x_2&=-6.561443673\\x_3&=-6.535451368\end{aligned}`

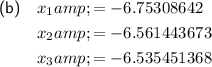
(c) Approximations to the location of one of the roots of the equation given in part (a).

Explanation:

Part (a)

Given equation:

`20-x^3-7x^2=0`

Add x³ to both sides of the equation:

`\implies 20-x^3-7x^2+x^3=0+x^3`

`\implies 20-7x^2=x^3`

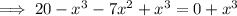
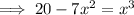
Divide both sides of the equation by x²:

`\implies (20)/(x^2) -(7x^2)/(x^2) =(x^3)/(x^2)`

`\implies (20)/(x^2) -7 =x`

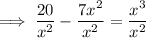
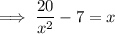
Part (b)

Given recursive rule:

`\begin{cases}x_(n+1)=\frac{20}{x_n{^2}}-7\\x_0=-9\end{cases}`

Therefore:

`\begin{aligned}\implies x_1&=\frac{20}{x_0{^2}}-7\\\\&=(20)/((-9)^2)-7\\\\&=(20)/(81)-7\\\\&=(20)/(81)-(567)/(81)\\\\&=(20-567)/(81)\\\\&=-(547)/(81)\\\\&=-6.75308642\end{aligned}`

`\begin{aligned}\implies x_2&=\frac{20}{x_1{^2}}-7\\\\&=(20)/(\left(-(547)/(81)\right)^2)-7\\\\&=(20)/(\left((299209)/(6561)\right))-7\\\\&=(131220)/(299209)-7\\\\&=(131220)/(299209)-(2094463)/(299209)\\\\&=-(1963243)/(299209)\\\\&=-6.561443673\end{aligned}`

`\begin{aligned}\implies x_3&=\frac{20}{x_2{^2}}-7\\\\&=(20)/(\left(-6.561443673\right)^2)-7\\\\&=(20)/(\left(43.05254308\right))-7\\\\&=0.4645486322-7\\\\&=-6.535451368\end{aligned}`

Part (c)

The values x₁, x₂ and x₃ are approximations to the location of one of the roots (zeros) of the equation given in part (a).

Each iteration gives a slightly more accurate value of a root x.