Question

At a certain school, the distribution of sleep (in hours is normally distributed with a mean of 7.5 hours and a standard deviation of 0.75 hours. what amount of sleep is at the 97.5th percentile of this distribution?

a. 7.5 hours
b. 8.25 hours
с. 9 hours
d. 9.75 hours

Answer 1

The amount of sleep at the 97.5th percentile of this distribution is approximately 8.97 hours.

Step-by-step explanation:

To find the amount of sleep at the 97.5th percentile, we need to find the z-score corresponding to that percentile and then convert it back to hours using the formula z = (x - mean) / standard deviation.

Z = (x - 7.5) / 0.75

By looking up the z-score corresponding to the 97.5th percentile in a standard normal distribution table, we find that it is approximately 1.96. Plugging this value into the formula and solving for x, we get:

1.96 = (x - 7.5) / 0.75

x - 7.5 = 1.96 * 0.75

x - 7.5 = 1.47

x = 7.5 + 1.47

x ≈ 8.97

Therefore, the amount of sleep at the 97.5th percentile of this distribution is approximately 8.97 hours. The closest answer choice is d. 9.75 hours.

Answer 2

the answer is b. 8.25 hours. Therefore, option b is correct

To find the amount of sleep at the 97.5th percentile of this normal distribution, you can use the Z-score formula and then convert the Z-score back to the original value. Here are the steps:

Step 1: Find the Z-score for the 97.5th percentile.

The Z-score formula is given by:

`\[Z = \frac{X - \mu}`
`{\sigma}`

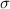
Where:

-
`\(Z\)` is the Z-score.

-
`\(X\)` is the value from the distribution.

-
`\(\mu\)` is the mean of the distribution.

-
`\(\sigma\)` is the standard deviation of the distribution.

In this case, \(\mu = 7.5\) hours, \(\sigma = 0.75\) hours, and we want to find \(X\) for the 97.5th percentile, which corresponds to a Z-score of \(Z = 1.96\) (you can find this value using a standard normal distribution table or calculator).

So, plug in the values:

`\[1.96 = (X - 7.5)/(0.75)\]`

Step 2: Solve for \(X\):

First, multiply both sides of the equation by 0.75 to isolate \(X\):

`\[0.75 \cdot 1.96 = X - 7.5\]`

Now, add 7.5 to both sides to find \(X\):

`\[X = 7.5 + (0.75 \cdot 1.96)\]`

Calculate the right side:

`\[X = 7.5 + 1.47\]`

Step 3: Calculate
`\(X\)`:

`\[X = 8.97\]`

So, the amount of sleep at the 97.5th percentile of this distribution is approximately 8.97 hours.

Now, let's round this to the nearest option:

b. 8.25 hours.

So, the answer is b. 8.25 hours.