Question

You wish to test the following claim (H₁​) at a significance level of α=0.05.

H0​:μ=76.1
H1​:μ≠76.1​
You believe the population is normally distributed, but you do not know the standard deviation. You obtain a sample of size n=24 with mean xˉ=82 and a standard deviation of s=9.4. What is the test statistic for this sample? (Report answer accurate to three decimal places.)
test statistic =

Answer 1

The test statistic for this sample is approximately 3.191.

Step-by-step explanation:

To calculate the test statistic for this hypothesis test, you would use the formula for the t-test for a population mean when the population standard deviation is unknown. The formula is given by
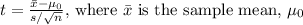`\( t = \frac{{\bar{x} - \mu_0}}{{s/√(n)}} \), where \( \bar{x} \) is the sample mean, \( \mu_0 \)`is the hypothesized population mean under the null hypothesis, s is the sample standard deviation, and n is the sample size.

In this case,
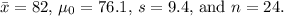`\( \bar{x} = 82 \), \( \mu_0 = 76.1 \), \( s = 9.4 \), and \( n = 24 \).`Plugging these values into the formula, you get
`\( t = \frac{{82 - 76.1}}{{9.4/√(24)}} \),` which simplifies to approximately 3.191.

The test statistic measures how many standard errors the sample mean is away from the hypothesized population mean. In this context, a larger test statistic indicates stronger evidence against the null hypothesis. The critical value for a two-tailed test at a significance level of 0.05 with 23 degrees of freedom is approximately 2.069. Since 3.191 is greater than 2.069, you would reject the null hypothesis and conclude that there is significant evidence to support the claim
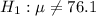`\( H_1: \mu \\eq 76.1 \)` at the 0.05 significance level.