Question

In Exercises 41-44,

(a) does the equation Ax=0 have a nontrivial solution and
(b) does the equation Ax=b have at least one solution for every possible b?
41. A is a 3×3 matrix with three pivot positions.
42. A is a 3×3 matrix with two pivot positions.
43. A is a 3×2 matrix with two pivot positions.
44. A is a 2×4 matrix with two pivot positions.

Answer 1

• For a consistent system, the number of pivot positions should be equal to the number of variables (rows = columns).
• If the number of pivot positions is less than the number of variables, the system is inconsistent, and there exists a nontrivial solution to
  `\(Ax = 0\).`
• The consistency of
  `\(Ax = b\)` depends on the number of pivot positions. If there are enough pivot positions, the system is consistent for every possible \(b\); otherwise, it is inconsistent.

Explanation:

Let's analyze each case:

41. A is a 3×3 matrix with three pivot positions.

(a) No, the equation
`\(Ax = 0\)` does not have a nontrivial solution. Since there are three pivot positions, the system is consistent, and the only solution is the trivial solution
`(\(x = 0\)).`

(b) Yes, the equation
`\(Ax = b\)` has at least one solution for every possible
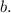`\(b\).` The system of equations is consistent, and since there are three pivot positions, the system is determined, and there is a unique solution for each
`\(b\).`

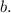
42. A is a 3×3 matrix with two pivot positions.

(a) Yes, the equation
`\(Ax = 0\)` has a nontrivial solution. Since there are fewer pivot positions (two) than the number of variables (three), the system is inconsistent, and there exists a nontrivial solution.

(b) No, the equation
`\(Ax = b\)` does not have at least one solution for every possible b. The system is inconsistent, and not all right-hand side vectors b will have a solution.

43. A is a 3×2 matrix with two pivot positions.

(a) Yes, the equation
`\(Ax = 0\)` has a nontrivial solution. Since there are fewer columns (2) than rows (3), the system is inconsistent, and there exists a nontrivial solution.

(b) No, the equation
`\(Ax = b\)` does not have at least one solution for every possible b. The system is inconsistent.

44. A is a 2×4 matrix with two pivot positions.

(a) Yes, the equation
`\(Ax = 0\)` has a nontrivial solution. Since there are fewer pivot positions (two) than the number of variables (four), the system is inconsistent, and there exists a nontrivial solution.

(b) No, the equation
`\(Ax = b\)` does not have at least one solution for every possible b. The system is inconsistent.