The period of the given sine function is approximately 0.106 hours, and the cruise ship can safely dock for approximately 2.428 hours in each period, with safe docking intervals occurring around
 to
to
 hours and
hours and
 to
to
 hours.
hours.
Certainly! Let's break down the given information and calculations step by step:
A) Finding the Period of the Sine Function:
1. Given Sine Function:
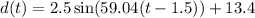
2. Frequency Determination:
The coefficient of
 inside the sine function is 59.04, which determines the frequency of the function.
inside the sine function is 59.04, which determines the frequency of the function.
3. Calculating Period:
The period
 of a sine function can be found by dividing
of a sine function can be found by dividing
 by the frequency:
by the frequency:
![\[ T = \frac{2\pi}{\text{Frequency}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1tltmxkwfnz1se3w1aszbfuz2qf6d3mjmg.png)
![\[ T = (2\pi)/(59.04) \approx 0.106 \text{ hours} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/grgdz6hw85p70cd6j5rpkm3tnbezvpsjux.png)
B) Determining Safe Docking Period:
1. Inequality Setup:
We want to find the values of
 . Set up the inequality:
. Set up the inequality:
![\[ 2.5 \sin(59.04(t-1.5)) + 13.4 \geq 12 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2c7whts6ke5a6k98cy9oqudtq2q8hyxw8o.png)
2. Solving for
 :
:
Subtract 13.4 from both sides and divide by 2.5:
![\[ \sin(59.04(t-1.5)) \geq -0.24 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5pt55lsa8m2py55c0t4kah35b1eq4k4pd4.png)
3. Inverse Sine Function:
Use the inverse sine function to find values of \(t\):
![\[ t-1.5 = \sin^(-1)(-0.24) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bg1djehy0zgbwolji82nj7vbg9yg46n6ej.png)
![\[ t \approx 1.458 \text{ hours} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/brb1ra65r4fisutiy6dxecfb935usy2w9p.png)
There may be another solution, considering the periodic nature of the sine function. To find additional solutions, add the period
 to the first solution:
to the first solution:
![\[ t \approx 1.458 + 0.106 \approx 1.564 \text{ hours} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zttkg3863u28gedi3jrlaoyy8pnml13umv.png)
![\[ t \approx 1.564 + 0.106 \approx 1.67 \text{ hours} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/o8acqafkw21sl4uom4bm8d90fu0dzwhohe.png)
Continue until you find a solution beyond the desired docking time.
Repeat the process for the second solution:
![\[ t \approx 3.886 + 0.106 \approx 3.992 \text{ hours} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vgnh6yieou6xvegr96d2pte73978qmhi6s.png)
![\[ t \approx 3.992 + 0.106 \approx 4.098 \text{ hours} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6wepvxvfx697pwv4shjuhy1nbyxnva819x.png)
4. Safe Docking Period:
The cruise ship can safely dock during the time intervals between these solutions. The duration of safe docking is approximately
 hours in each period.
hours in each period.