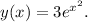Final Answer:
The solution to the initial value problem
 , with the initial condition
, with the initial condition
Step-by-step explanation:
To solve the given initial value problem, we can use separation of variables. Start by separating variables and integrating both sides:
![\[ (1)/(y) \, dy = 2x \, dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/t2ecw7eaom72k7buuqo4slmrzy3uks4pr6.png)
Integrate both sides:
![\[ \ln|y| = x^2 + C \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kjaeav6upg6281ph0neo94zhjusp02tyol.png)
Now, apply the initial condition
 :
:
![\[ \ln|3| = 0 + C \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6lu5b9ny859de2rr209ifgteud031disqc.png)
![\[ C = \ln|3| \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/sooueubk9vjcrua06ydl490ydokfvfhjaf.png)
Substitute
 back into the equation:
back into the equation:
![\[ \ln|y| = x^2 + \ln|3| \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ftge4orxyst4kcw7vomub6843cqcr3u3ey.png)
Exponentiate both sides:
![\[ |y| = 3e^(x^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/irn51n9yal3xn4olm782825lx8m3bnng7p.png)
Consider the absolute value, and since
 is positive:
is positive:
![\[ y(x) = 3e^(x^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ln9c8yis98y7a666bc6peenfhb19yohgpc.png)
This is the solution to the initial value problem. The exponential term
 reflects the growth of the solution, and the initial condition ensures that the constant
reflects the growth of the solution, and the initial condition ensures that the constant
 is determined, resulting in the specific solution
is determined, resulting in the specific solution