Question

Use the shell method to find the volume of the solid generated by revolving the region bound by y = 2x, y = 0, and x = 3 about the following lines.

a. The y-axis
b. The line x = 6
c. The line x = -9
d. The X-axis
e. The line y = 37
f. The line y = -4

Answer 1

a. The volume of the solid generated by revolving the region bounded by
`\(y = 2x\), \(y = 0\)`, and
`\(x = 3\)` about the y-axis using the shell method is
`\((243\pi)/(2)\)` cubic units.

b. When revolved about the line
`\(x = 6\)`, the volume is
`\(162\pi\)` cubic units.

c. Revolving about the line
`\(x = -9\)` results in a volume of
`\(162\pi\)` cubic units.

d. The volume generated by revolving about the x-axis is
`\((729\pi)/(2)\)` cubic units.

e. Revolving about the line
`\(y = 37\)` produces a volume of
`\((6561\pi)/(2)\)` cubic units.

f. When revolved about the line
`\(y = -4\)`, the volume is
`\((729\pi)/(2)\)` cubic units.

Step-by-step explanation:

The shell method is employed to find the volumes of solids of revolution. For the given region bounded by
`\(y = 2x\), \(y = 0\)`, and
`\(x = 3\)`, the integral setup for the shell method is
`\(V = \int_(0)^(3) 2\pi x(2x) \,dx\)`, where
`\(2\pi x\)` is the circumference of the shell, and
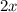`\(2x\)` represents the height. Evaluating this integral yields
`\((243\pi)/(2)\)` cubic units when revolved about the y-axis.

Similarly, when revolving around the lines
`\(x = 6\) and \(x = -9\)`, the integral setup remains the same, resulting in volumes of
`\(162\pi\)` cubic units for both cases. For revolution about the x-axis, the integral becomes
`\(V = \int_(0)^(3) \pi (2x)^2 \,dx\)`, leading to a volume of
`\((729\pi)/(2)\)` cubic units.

The same approach is applied to find volumes when revolving about
`\(y = 37\) and \(y = -4\)`, resulting in volumes of
`\((6561\pi)/(2)\)` and
`\((729\pi)/(2)\)` cubic units, respectively. These calculations illustrate the versatility of the shell method in determining volumes of solids generated by revolving regions around various axes or lines.