(a) The exponential function
 can be rewritten as
can be rewritten as
 , where
, where
 . (b) The annual decay rate is approximately 6.51% per year (rounded to the nearest 0.01%). (c) The continuous decay rate is approximately -6.72% per year (rounded to the nearest 0.01%).
. (b) The annual decay rate is approximately 6.51% per year (rounded to the nearest 0.01%). (c) The continuous decay rate is approximately -6.72% per year (rounded to the nearest 0.01%).
(a) To rewrite the exponential function
 in the form
in the form
 , recognize that
, recognize that
 . Therefore,
. Therefore,
![\[y = 400e^(-0.07t) = 400(b^t) \]](https://img.qammunity.org/2024/formulas/mathematics/college/xxjjdkh83o7qbqlkvl15t4rn58c44iiwdz.png)
(b) Calculate the value of b using
 :
:
![\[b = e^(-0.07) \approx 0.9349\]](https://img.qammunity.org/2024/formulas/mathematics/college/kovoga6p2zmu69e9g7xwsxx406yrwelft6.png)
The exponential function is decaying because the base (b) is between 0 and 1.
(c) For the annual growth/decay rate r, use the formula r = |1 - b| and multiply by 100 to express as a percentage:
Annual decay rate =

For the continuous growth/decay rate, use the natural logarithm ln of b, multiplied by 100:
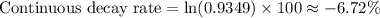
The negative sign indicates decay in both cases, as mentioned.