Question

(b) v = r2×2 as a real vector space, u = {a ∈ r2×2 : a2 = 0}

Answer 1

To find a cubic Hermite curve as Curve B in both the matrix and algebraic forms, we can use the given starting and ending points and tangent vectors. To find the modified curve as Curve C, we can scale the tangent vectors by a factor of 6 while keeping the directions and the starting and ending points unchanged, and then use the same formulas as above to find the modified curve in both the matrix and algebraic forms.

Explanation:

Based on the given information, we are asked to find a cubic Hermite curve as Curve B in both the matrix and algebraic forms, and then find the modified curve as Curve C by scaling the vectors by a factor of 6 while keeping the directions and the starting and ending points unchanged.

A cubic Hermite curve is a type of parametric curve that is defined by two points and two tangent vectors at those points. The matrix form of a cubic Hermite curve is:

`$$\begin{bmatrix} x(t) \\ y(t) \end{bmatrix} = \begin{bmatrix} 2t^3 & -3t^2 & 0 & 1 \\ t^3 & -2t^2 & t & 0 \end{bmatrix} \begin{bmatrix} x_0 \\ x_1 \\ v_0 \\ v_1 \end{bmatrix}$$`

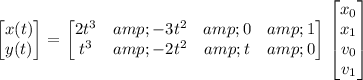
where (x0, y0) and (x1, y1) are the starting and ending points of the curve, and (v0, v1) are the tangent vectors at those points.

The algebraic form of a cubic Hermite curve is:

`x(t) &= (2t^3 - 3t^2 + 1)x_0 + (-2t^3 + 3t^2)x_1 + (t^3 - 2t^2 + t)v_0 + (t^3 - t^2)v_1 \\y(t) &= (2t^3 - 3t^2 + 1)y_0 + (-2t^3 + 3t^2)y_1 + (t^3 - 2t^2 + t)w_0 + (t^3 - t^2)w_1\end{aligned}$$`

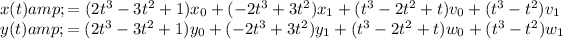
where (x0, y0) and (x1, y1) are the starting and ending points of the curve, and (v0, w0) and (v1, w1) are the tangent vectors at those points.

To find the modified curve as Curve C, we need to scale the tangent vectors by a factor of 6 while keeping the directions and the starting and ending points unchanged. Therefore, the modified tangent vectors are:

`$$\begin{aligned}v_0' &= 6v_0 \\v_1' &= 6v_1\end{aligned}$$`

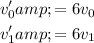
Using these modified tangent vectors, we can find the modified curve as Curve C in both the matrix and algebraic forms using the same formulas as above.

In summary, to find a cubic Hermite curve as Curve B in both the matrix and algebraic forms, we can use the given starting and ending points and tangent vectors. To find the modified curve as Curve C, we can scale the tangent vectors by a factor of 6 while keeping the directions and the starting and ending points unchanged, and then use the same formulas as above to find the modified curve in both the matrix and algebraic forms.