Question

Find the area of the surface obtained by rotating the curve y³=x about the y-axis for 1≤y≤4.

Answer 1

The area of the surface formed by rotating the curve y³=x about the y-axis for 1≤y≤4 is A = 48π square units.

Step-by-step explanation:

Given curve: y³ = x

To find the surface area formed by rotating this curve about the y-axis within the interval 1 ≤ y ≤ 4, use the formula for surface area of revolution:

`\[ A = 2π \int_(1)^(4) f(y) √(1 + (f'(y))^2) dy \]`

Given the curve y³ = x, express x in terms of y:
`x = y^(2/3)`.

Find the derivative of x with respect to
`y: \( (dx)/(dy) = (2)/(3) y^(-1/3) \)`.

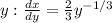Substitute these values into the surface area formula:

`\[ A = 2π \int_(1)^(4) y^(2/3) \sqrt{1 + \left((2)/(3) y^(-1/3)\right)^2} dy \]`

Simplify the integrand and solve for the surface area. Introduce a substitution where
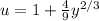`\( u = 1 + (4)/(9)y^(2/3) \)`, which transforms the integral to:

`\[ A = 2π \int_(13/9)^(25/9) u^(1/2) du \]`

Integrate with respect to u:

`\[ A = 2π \left[(2)/(3) u^(3/2)\right]_(13/9)^(25/9) \]`

After evaluating the integral, the final result is:

`\[ A = 48π \]`

Therefore, the surface area obtained by rotating the curve y³ = x about the y-axis for 1 ≤ y ≤ 4 is 48π square units.