Question

In Question 1, what would the degrees of freedom of our test statistic be (before using the t-Table)?

Question 1 was: Doctors recommend having a total cholesterol level below 200 mg/dL and consider anything greater than that value to be too high. Suppose that a sample of 36 people is taken whose mean cholesterol level is 225 mg/dL with a standard deviation of 62 mg/dL. If we were looking for evidence that the population mean cholesterol level - or u - is too high, what would our Hypotheses be in terms of u?

Answer 1

Based on the above, the degrees of freedom would be 35.

From the question, hypothesis for the above can be:

Null Hypothesis
`(\(H_0\)): \( \mu \leq \text{specified value}\)`

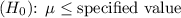
Alternative Hypothesis
`(\(H_1\) or \(H_a\)): \( \mu > \text{specified value}\)`

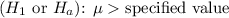
So, your hypotheses would be:

Null Hypothesis
`(\(H_0\)):`
`\( \mu \leq 200 \) (doctors recommend having a total cholesterol level below 200 mg/dL)`

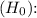
Alternative Hypothesis
`(\(H_1\)): \( \mu > 200 \) (looking for evidence that the population mean cholesterol level is too high)`

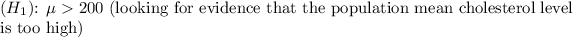
The degrees of freedom for a one-sample t-test is equal to n - 1, where n is the sample size.

In this case, n = 36, so the degrees of freedom would be:

36 - 1 = 35.