Question

The cost of a pound of strawberries at a local market increases at a rate of 2.1% per year due to greater agricultural costs. The following exponential expression gives the cost of a pound of strawberries after t years. 3.50(1.021)^t

Which of the following expressions reveals the monthly rate of increase for the cost of a pound of strawberries?

Answer 1

(1.002)12t.

Explanation:

he expression, (1.021)t, reveals the rate of increase for the cost of a pound of strawberries per year.

In order to reveal the monthly rate of increase, rewrite the expression in terms of months. Since there are 12 months in a year, raise the growth factor for the year to the power in order to find the growth factor for the month. To keep this expression equivalent to the given expression, the exponent outside the parentheses needs to change to 12t.

Therefore, the expression that reveals the monthly rate of increase for the cost of a pound of strawberries is (1.002)12t.

Answer 2

1 - (1.021)^(1/12) ≈ 0.17 %

Explanation:

In the given expression 3.50 is the initial value (cost per pound at the time of the first recording) and (1.021)^t is the increase factor for a given time difference since first recording (in years).

Putting
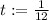`t := {(1)/(12)}` into that expression yields the increase factor per month and subtracting it from 1 yields the “rate” notation which is just the part that was “added” to the initial amount.

Bonus:
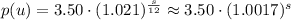`p(u) = 3.50 \cdot (1.021)^(s)/(12) \approx 3.50 \cdot (1.0017)^s` is the cost function for a given time
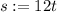`s := 12 t` in months.

Note that this approach gives you an increase rate based on an average month length. It doesn’t consider that a real month has different amount of days. For example “s = 3” means “3/12 of a year”, or “1/4 of a year” as opposed to something like “June 13 till September 13”.