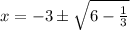Question

3x(x + 6) = -10

Enter your solution in the exact, most simplified form. If there are two solutions, write the answer using the ± symbol. DESCRIBE AND JUSTIFY THE METHODS YOU USED TO SOLVE THE QUADRATIC EQUATION!

Answer 1

I think it's x = - 9 - √51/3 , -9 + √51/3

Answer 2

Explanation:

Expand it:
`3x^2 + 18x = -10`

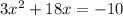
Add 10 to both sides:
`3x^2 + 18x + 10 = 0`

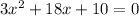
Divide both sides by 3:
`x^2 + 6x + (10)/(3) = 0`

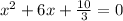
Find a, b for
`(x + a)^2 + b = x^2 + 2x + a^2 + b \overset{!}{=} x^2 + 6x + (10)/(3)`

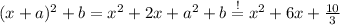
It’s
`a = (6)/(2) = 3 \land b = (10)/(3) - a^2 = 3 + (1)/(3) - 9 = -6 + (1)/(3)`

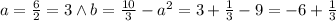
So, inserting it leads to:
`(x+3)^2 -6 + (1)/(3) = 0`

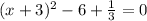
Subtract b from both sides:
`(x+3)^2 = 6-(1)/(3)`

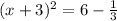
Apply square root to both sides and consider the two solutions:
`x + 3 = \pm\sqrt{6-(1)/(3)}`

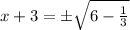
Subtract 3 from both sides and you get
`x = -3 \pm \sqrt{6 - (1)/(3)}`