Question

You have decided that you want to be a millionaire when you retire in 44 years.

a) If you can earn an annual return of 11.22 per cent, how much do you have to invest today?
b) What if you can earn an annual return of 5.61 per cent?

Answer 1

Main Answer:

a) To determine how much you need to invest today to become a millionaire in 44 years with an annual return of 11.22 percent.

b) Similarly, if the annual return is 5.61 percent, the initial investment required can be calculated.

Step-by-step explanation:

a) To calculate the present value of a future sum, we can use the present value formula:

`\[ PV = (FV)/((1 + r)^n) \]`

Where:

`\( PV \)` is the present value (amount to be invested today),

`\( FV \)` is the future value (desired amount at retirement),

`\( r \)` is the annual interest rate (in decimal form),

`\( n \)` is the number of years.

In this case,
`\( FV \)` is one million dollars,
`\( r \)` is 11.22 percent (0.1122 in decimal form), and
`\( n \)` is 44 years.

b) Using the same formula, we can calculate the present value for an annual return of 5.61 percent.

Detailed calculations:

a) For an annual return of 11.22 percent:

`\[ PV = (1,000,000)/((1 + 0.1122)^(44)) \]`

b) For an annual return of 5.61 percent:

`\[ PV = (1,000,000)/((1 + 0.0561)^(44)) \]`

Now, let's compute these values to find out the required initial investments.

a)
`\( PV = (1,000,000)/((1 + 0.1122)^(44)) \)`

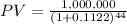
b)
`\( PV = (1,000,000)/((1 + 0.0561)^(44)) \)`

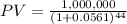
So, the final answers will be the calculated values of
`\( PV \)` for each scenario.