Question

A wheel is rotating at radians per second, and the wheel has a -inch diameter. What is the speed of a point on the rim?

Answer 1

The speed of a point on the rim of the rotating wheel is
`\( (1)/(2) \pi \)`times the angular speed multiplied by the diameter.

Step-by-step explanation:

The speed of a point on the rim of a rotating wheel is determined by the product of the angular speed and the distance from the center of rotation to the point. In this case, the angular speed is given in radians per second, denoted by \( \omega \), and the distance from the center to the rim is the radius of the wheel, which is half the diameter. The formula for linear speed
`(\(v\)) is \(v = \omega * r\), where \(r\)` is the radius. However, since the diameter is given, we use
`\(r = (1)/(2) * \text{diameter}\).`

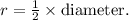
To derive the final formula, substitute
`\(r = (1)/(2) * \text{diameter}\)` into the linear speed formula:

`\[ v = \omega * \left((1)/(2) * \text{diameter}\right) \]`

Simplifying, we find that the speed
`(\(v\)) is equal to \( (1)/(2) \pi \)`times the angular speed
`(\(\omega\))` multiplied by the diameter. This result is based on the relationship between linear speed, angular speed, and the dimensions of the rotating object. The factor
`\( (1)/(2) \pi \)` arises from the conversion between radians and circular distance on the wheel's rim. Thus, the final formula succinctly expresses the speed of a point on the rim in terms of the given angular speed and diameter.