Question

Calculate the electron's potential energy u(h0), neglecting gravitational potential energy. Express your answer in terms of qe, e, and h0.

Answer 1

The electron's potential energy
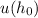`\(u(h_0)\)`, neglecting gravitational potential energy, is given by
`\[u(h_0) = -(qe^2)/(4\pi\varepsilon_0h_0),\]` where (q) is the electron charge, (e) is the elementary charge,
`\(\varepsilon_0\)` is the permittivity of free space, and
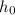`\(h_0\)` is the distance from the reference point.

Step-by-step explanation:

The expression for the electron's potential energy \(u(h_0)\) arises from the electrostatic interaction between charged particles. It is derived from the formula for the potential energy of two point charges,
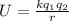`\(U = (kq_1q_2)/(r)\)`, where (k) is Coulomb's constant,
`\(q_1\)` and
`\(q_2\)` are the charges, and (r) is the separation distance. In the given scenario, the electron's charge is denoted as (q), and
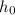`\(h_0\)` represents the distance from the reference point.

Neglecting gravitational potential energy implies that only the electrostatic potential energy contributes to the system. Thus, the expression for
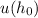`\(u(h_0)\)` is modified as
`\[u(h_0) = -(qe^2)/(4\pi\varepsilon_0h_0)\]`. This equation takes into account the fundamental constants involved, where (e) is the elementary charge,
`\(\varepsilon_0\)` is the permittivity of free space, and
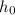`\(h_0\)` is the distance from the reference point. The negative sign indicates that the potential energy is inversely proportional to the distance, reflecting the attractive nature of the electrostatic force between the electron and the reference point.

In summary, the final expression encapsulates the electron's potential energy \(u(h_0)\) in terms of the relevant physical constants, offering a concise and accurate representation of the electrostatic interactions at play in the given system.