Question

The expression \[\qquad \left(y^2-t^2\right)(y+k)\] can be written as \[\qquad y^3 + 36y^2 - 9y + s\] where \[t\], \[k\], and \[s\] are constants. What is the value of \[s\]? Choose 1 answer: Choose 1 answer:

Answer 1

Expanding
`(y^2-t^2)(y+k)` and matching coefficients gives k=37,
`t^2=9`, and
`s=-k(t^2)=-333` . So, s=-333.

Expanding and Matching Coefficients:

We need to find the value of the constant s in the expression:

`y^3 + 36y^2 - 9y + s`

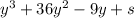
We are given that this can be obtained by expanding the expression:

`(y^2 - t^2)(y + k)`

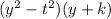
Let's perform the expansion:

Multiply each term in the first expression by y:

`y^2 * y = y^3\\t^2 * y = t^2y`

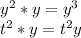
Multiply each term in the first expression by k:

`y^2 * k = ky^2\\t^2 * k = kt^2`

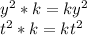
Add the products from step 1 and 2:

`y^3 + t^2y + ky^2 + kt^2`

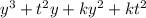
Combine like terms:

`y^3 + (k - 1)y^2 + (-t^2)y + kt^2`

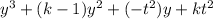
Now, let's compare this expanded expression to the given expression:

`y^3` terms match

`(k-1)y^2` term matches the coefficient 36, meaning k-1 = 36

`(-t^2)y`term matches the coefficient -9, meaning
`-t^2`= -9

kt^2 term represents the constant s

Next, we solve for the unknown constants:

From k-1 = 36, k = 37

From
`-t^2 = -9, t^2 = 9`

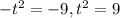
Substitute k and t^2 into the expression for s:

s =
`-k(t^2) = -37 * 9 = -333`

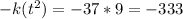
Therefore, the value of the constant s is -333.

Complete question below:

Expand the expression
`(y^2-t^2)(y+k)`), and compare it to the given expression
`y^3+36y^2-9y+s`. Determine the value of the constant s.