Question

Need help for Geometry

Answer 1

Direct answer :

`\color{plum} \: x \: \bold{ \tt \: = \: 11}`

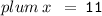
Steps to derive the correct answer :

Given :

• segment AB = segment DE
• segment BC = segment EF
• segment AC = segment DF

Since all sides are equal triangle ABC is congruent to triangle DEF under the SSS congruence criterion.

m∠B = (92+y)°

m∠E = (6y-28)°

We know that :

• angle B = angle E

Which means :

`= \tt92 + y = 6y - 28`

`=\tt 92 = 6y - 28 - y`

`=\tt 92 = 5y - 28`

`= \tt92 + 28 = 5y`

`= \tt120 = 5y`

`=\tt y = (120)/(5)`

`=\tt y = 24`

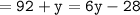
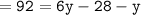
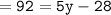
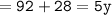
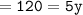
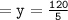
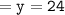
Thus, the value of y = 24

Then :

angle B :

`=\tt 92 + y`

`=\tt 92 + 24`

`= \tt116`

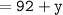
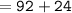
Thus, the measure of angle B = 116

angle E :

`= \tt6y - 28`

`=\tt 6 * 24 - 28`

`=\tt 144 - 28`

`=\tt 116`

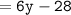
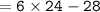
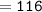
Thus, the measure of angle E = 116

Since the measure of both these angles is equal we can conclude that we have found out their correct measures.

measure of segment AC = 2x + 47

Measure of segment DF = 6x + 3

• Segment AC = Segment EF

Which means :

`= \tt6x + 3 = 2x + 47`

`= \tt6x + 3 - 2x = 47`

`= \tt4x + 3 = 47`

`\tt4x = 47 - 3 \\ 4x = 44`

`=\tt x = (44)/(4)`

`=\tt x = 11`

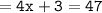
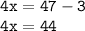
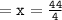
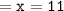
Thus, the value of x = 11

Let us check whether or not we have found out the correct value of x by placing 11 in the place of x :

`= \tt6 * 11 + 3 = 11 * 2 + 47`

`=\tt 66 + 3 = 22 + 47`

`=\tt 69 = 69`

• m∠B = 69°
• m∠C = 69°

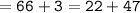
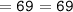
Therefore, the value of x = 11