Variables:
 (1st booster time),
(1st booster time),
 (5th booster time = 35 days),
(5th booster time = 35 days),
 (batch size),
(batch size),
 (cumulative units),
(cumulative units),
 (learning curve ratio),
(learning curve ratio),
 (10th booster time). Theoretical formula:
(10th booster time). Theoretical formula:
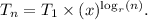
Let's define the variables based on the information provided:
Given information:
-
 : Time required for the 1st refurbished first stage booster (unknown)
: Time required for the 1st refurbished first stage booster (unknown)
-
 : Time required for the 5th refurbished first stage booster = 35 workdays
: Time required for the 5th refurbished first stage booster = 35 workdays
-
 : Batch size = 5 (as data is available for the 5th refurbished unit)
: Batch size = 5 (as data is available for the 5th refurbished unit)
-
 : Cumulative production units completed (unknown)
: Cumulative production units completed (unknown)
-
 : Learning curve ratio
: Learning curve ratio
-
 : Time required for the 10th refurbished first stage booster (unknown)
: Time required for the 10th refurbished first stage booster (unknown)
Learning curve formula:
![\[ T_n = T_1 * (x)^(\log_r(n)) \]](https://img.qammunity.org/2024/formulas/business/college/a8bp2mybisb5k0jqqr00s0z7xl78gchzsc.png)
Now, let's substitute the given values and the unknowns into the formula:
![\[ 35 = T_1 * (5)^(\log_r(5)) \]](https://img.qammunity.org/2024/formulas/business/college/lcoeu1djsq7gsp9kwoo10lwmv8r7kdga8p.png)
This formula is used to calculate the time for the 5th refurbished first stage booster. To solve for
 , you would need to rearrange the equation and solve for
, you would need to rearrange the equation and solve for
Now, the learning curve ratio
 is given as 90% and 95%, so you will use these ratios to calculate
is given as 90% and 95%, so you will use these ratios to calculate
 based on the cumulative production units completed
based on the cumulative production units completed
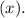
The theoretical formula for calculating
![\( T_(10) \) is:\[ T_(10) = T_1 * (10)^(\log_r(10)) \]](https://img.qammunity.org/2024/formulas/business/college/ydaw6483zidtmiedrf9iapg44nko3e7o1z.png)
Now, you can use this formula twice, once with a 90% learning curve ratio and once with a 95% learning curve ratio, to calculate the theoretical time for the 10th refurbished first stage booster in each case.