Direct answers :
In triangle 1 :
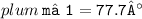
In triangle 2 :
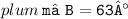
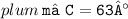
In triangle 3 :
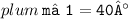

Steps to derive the correct measurement of each of the angles :
In triangle 1 :
Given :
Sum of all angles in a triangle = 180°
Which means :


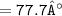
Thus, the measure of angle 1 = 77.7°
Since the sum of all angles (77.7+52.2+50.1=180°) equals 180° we can conclude that we have found out the correct value of angle 1.
Therefore, the m∠1 = 77.7°
In triangle 2 :
Given :
Let the measure of angle B be x.
Then, the measure of angle C will also be x.
Which means the sum of angle B and C will be equal to 2x.
That means :
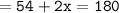
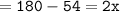


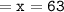
Thus, the measure of Angle B = 63°
Measure of angle C = 63°
In triangle 3 :
Given :
- m∠3 = 112°
- Measure of exterior angle = 140°
Which means :
= m∠2 + 112° = 140° (exterior angle property)
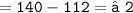
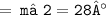
Thus, the measure of angle 2 = 28°
= m∠1 + m∠2 + m∠3 = 180°
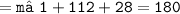

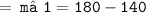
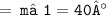
Thus, the measure of angle 1 = 40°