Question

The height H of an ball that is thrown straight upward from an initial position 3 feet off the ground with initial velocity of 90 ft./s is given by the equation H equals 3+90 T -16 T squared where t equals time in seconds. After how many seconds will the ball be 84 feet above the ground

Answer 1

The ball will be 84 feet above the ground 1.125 seconds and 4.5 seconds after launch.

Explanation:

Statement is incorrect. Correct form is presented below:

The height
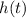`h(t)` of an ball that is thrown straight upward from an initial position 3 feet off the ground with initial velocity of 90 feet per second is given by equation
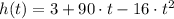`h(t) = 3 +90\cdot t -16\cdot t^(2)`, where
`t` is time in seconds. After how many seconds will the ball be 84 feet above the ground.

We equalize the kinematic formula to 84 feet and solve the resulting second-order polynomial by Quadratic Formula to determine the instants associated with such height:

`3+90\cdot t -16\cdot t^(2) = 84`

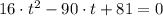`16\cdot t^(2)-90\cdot t +81 = 0` (1)

By Quadratic Formula:

`t_(1,2) = \frac{90\pm \sqrt{(-90)^(2)-4\cdot (16)\cdot (81)}}{2\cdot (16)}`

`t_(1) = 4.5\,s`,
`t_(2) = 1.125\,s`

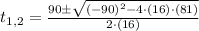
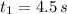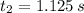
The ball will be 84 feet above the ground 1.125 seconds and 4.5 seconds after launch.