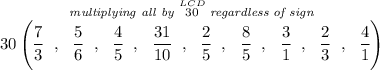keeping in mind that steeper for a slope means a higher number or a larger fraction regardless of negative or positive, so let's sort them out from small to high.
Now, let's make the integers a fraction, that 3 = 3/1 and 4 = 4/1, then let's get the LCD of all denominators, hmmm in this case the LCD is 30.
Let's multiply all fractions or values by the LCD of 30, what we'd get is in essence just the numerator of a fraction whose denominator is 30, then we can simply check which numerator is larger and sort them out :).