Question

What is the exact value of sine theta if cosine theta equals -3/4 and 90 < theta < 180

Answer 1

well, the hypotenuse is never negative, since it's simply the radius distance of the angle, so we can say that for this angle's cosine, the -(3/4) is really -3/4, so the "3" is the negative one, and we also know that 90° < θ < 180°, which is another way of saying, θ is in the II Quadrant.

`\cos(\theta )=\cfrac{\stackrel{adjacent}{-3}}{\underset{hypotenuse}{4}} \hspace{5em}\textit{now, let's find the \underline{opposite side}} \\\\\\ \begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies o=√(c^2 - a^2) \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{4}\\ a=\stackrel{adjacent}{-3}\\ o=opposite \end{cases}`

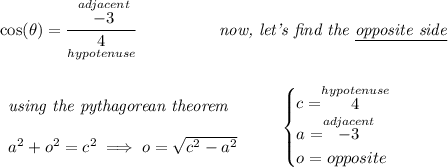
`o=\pm√( 4^2 - (-3)^2)\implies o=\pm√( 16 - 9 ) \implies o=\pm√( 7 )\implies \stackrel{ \textit{II Quadrant} }{o=√(7)} \\\\[-0.35em] ~\dotfill\\\\ ~\hfill~\sin( \theta )=\cfrac{\stackrel{opposite}{√(7)}}{\underset{hypotenuse}{4}} ~\hfill~`