Question

Solve for
\[t\]:


\[\dfrac{17}{20}=t+\left(-\dfrac{13}{20}\right)\]

Answer 1

Adding and simplifying, the equation becomes 30/20 - 13/20 = t. Solving, t = 4/20 simplified to 1/5.

Solving for t in
`(17)/(20)=t+\left((-13)/(20)\right):`

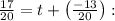
This equation represents a linear equation with one variable, t. To solve for t, we need to isolate it on one side of the equation.

Combining Fractions: We can combine the fractions on both sides of the equation by adding the fractions with the same denominator.

`(17)/(20) + (13)/(20) = t + (13)/(20) + (13)/(20)`

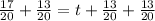
Adding the fractions on the left-hand side simplifies to
`(30)/(20)`.

Isolating t: We can now isolate t by subtracting the constant term from both sides of the equation.

`(30)/(20) - (13)/(20) - (13)/(20) = t`

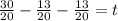
Subtracting the fractions on both sides gives us \frac{4}{20}.

Simplifying the Solution: We can now simplify the remaining fraction to its lowest terms by dividing the numerator and denominator by 4.

`(4)/(20) / (4)/(4) = (1)/(5)`

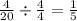
Therefore, the solution for t in the equation
`(17)/(20)=t+\left((-13)/(20)\right)` is t= 1/5.

Complete question below:

The given question is
`(17)/(20)=t+\left((-13)/(20)\right)`. We will need to solve a linear equation .