Question

A) Lora (of mass 57.1 kg) is an expert skier. She starts at 3.2 m/s at the top of the lynx run, which is 109 m above the bottom.

What is her final kinetic energy at the bottom of the ski run?
Answer in units of J.

B) What is her speed at the bottom?
Answer in units of m/s.

Answer 1

The skier's final kinetic energy at the bottom of the ski run is equal to her initial potential energy. Her final kinetic energy is approximately 60395.42 J. The skier's speed at the bottom of the ski run is approximately 45.9 m/s.

Step-by-step explanation:

To find the final kinetic energy of the skier at the bottom of the ski run, we can use the conservation of energy principle. At the top of the run, the skier has potential energy due to her height above the bottom. This potential energy is converted into kinetic energy as she skis down the slope. The formula for kinetic energy is
`KE = 1/2mv^2,` where m is the mass and v is the velocity. Since the skier starts from rest, her initial kinetic energy is zero. Therefore, her final kinetic energy at the bottom of the ski run is equal to her initial potential energy.

Using the formula for potential energy, PE = mgh, where m is the mass, g is the acceleration due to gravity and h is the height, we can calculate the potential energy at the top of the run.

`PE = (57.1 kg)(9.8 m/s^2)(109 m) = 60395.42 J`

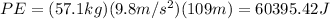
Therefore, the skier's final kinetic energy at the bottom of the ski run is 60395.42 J.

To find the skier's speed at the bottom of the run, we can use the formula for potential energy again. At the bottom of the run, the skier's height is zero, so her potential energy is also zero. This potential energy is converted into kinetic energy, so we can equate the two forms of energy.

KE = PE

`1/2mv^2 = mgh\\1/2(57.1 kg)v^2 = (57.1 kg)(9.8 m/s^2)(109 m)\\v^2 = 2(9.8 m/s^2)(109 m)\\v = sqrt(2(9.8 m/s^2)(109 m))`