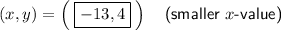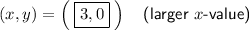Answer:
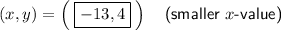
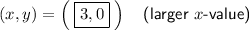
Explanation:
Given system of equations:
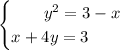
To solve by the method of substitution, rearrange the second equation to make x the subject:
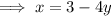
Substitute the found expression for x into the first equation and rearrange so that the equation equals zero:
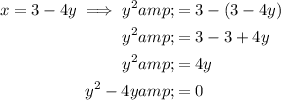
Factor the equation:
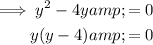
Apply the zero-product property and solve for y:
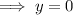
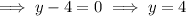
Substitute the found values of y into the second equation and solve for x:
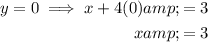
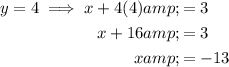
Therefore, the solutions are: