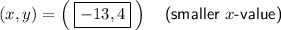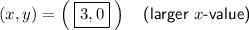Question

NO LINKS!! Use the method of substitution to solve the system. (if there's no solution, enter no solution). Part 3z​

Answer 1

`(x,y)=\left(\; \boxed{-13,4} \; \right)\quad \textsf{(smaller $x$-value)}`

`(x,y)=\left(\; \boxed{3,0} \; \right)\quad \textsf{(larger $x$-value)}`

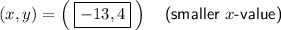
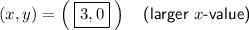
Explanation:

Given system of equations:

`\begin{cases}\;\;\;\;\;\;\;y^2=3-x\\x+4y=3\end{cases}`

To solve by the method of substitution, rearrange the second equation to make x the subject:

`\implies x=3-4y`

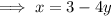
Substitute the found expression for x into the first equation and rearrange so that the equation equals zero:

`\begin{aligned}x=3-4y \implies y^2&=3-(3-4y)\\y^2&=3-3+4y\\y^2&=4y\\y^2-4y&=0\end{aligned}`

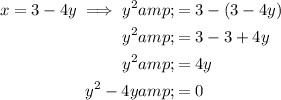
Factor the equation:

`\begin{aligned}\implies y^2-4y&=0\\y(y-4)&=0\end{aligned}`

Apply the zero-product property and solve for y:

`\implies y=0`

`\implies y-4=0 \implies y=4`

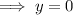
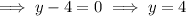
Substitute the found values of y into the second equation and solve for x:

`\begin{aligned}y=0 \implies x+4(0)&=3\\x&=3\end{aligned}`

`\begin{aligned}y=4 \implies x+4(4)&=3\\x+16&=3\\x&=-13\end{aligned}`

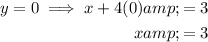
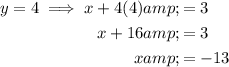
Therefore, the solutions are:

`(x,y)=\left(\; \boxed{-13,4} \; \right)\quad \textsf{(smaller $x$-value)}`

`(x,y)=\left(\; \boxed{3,0} \; \right)\quad \textsf{(larger $x$-value)}`

Answer 2

• (- 9, 4)
• (3, 0)

=====================

Given system

• y² = 3 - x
• x + 4y = 3

Rearrange equations

• x = 3 - y²
• x = 3 - 4y

Solve by elimination

• y² = 4y
• y² - 4y = 0
• y(y - 4) = 0
• y = 0 and y = 4

Find the value of x

• y = 0 ⇒ x = 3 - 0 = 3
• y = 4 ⇒ x = 3 - 4*3 = 3 - 12 = - 9