Question

NO LINKS!! An investment of P dollars increased to A dollars in t years. If interest was compounded continuously, find the interest rate. (Round your answer to the nearest whole number.)

A= 1822,. P= 1000,. t= 15

​

Answer 1

4% (nearest whole number)

Explanation:

Continuous Compounding Formula

`\large \text{$ \sf A=Pe^(rt) $}`

where:

• A = Final amount.
• P = Principal amount.
• e = Euler's number (constant).
• r = Annual interest rate (in decimal form).
• t = Time (in years).

Given values:

• A = $1,822
• P = $1,000
• t = 15 years

Substitute the given values into the formula and solve for r:

`\implies \sf 1822=1000 \cdot e^(15r)`

`\implies \sf (1822)/(1000)=e^(15r)`

`\implies \sf 1.822=e^(15r)`

`\implies \sf \ln 1.822=\ln e^(15r)`

`\implies \sf \ln 1.822=15r \ln e`

`\implies \sf \ln 1.822=15r`

`\implies \sf r=(\ln 1.822)/(15)`

`\implies \sf r=0.039995653...`

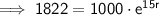
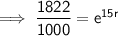
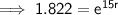
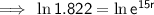
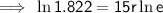
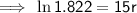
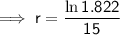
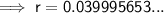
To convert into a percentage, multiply by 100:

`\implies \sf r=0.039995653... * 100`

`\implies \sf r=3.99995653...\%`

`\implies \sf r=4\%\; (nearest\;whole\;number)`

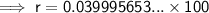
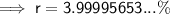
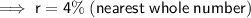
Therefore, the interest rate is 4% (nearest whole number).

Answer 2

• 4%

Explanation:

Use continuous compound equation:

• 
  `A = P*e^(rt)`, where A- future amount, P- invested amount, t- time, r- rate

Given

• A = $1822
• P = $1000,
• t = 15 years.

Plug in the values and solve for r

• 
  `1822 = 1000*e^(r*15)`
• 
  `e^(15r)=1822/1000`
• 
  `e^(15r)=1.822`
• 
  `ln\ e^(15r)=ln\ 1.822`
• 
  `15r=0.6`
• 
  `r=0.6/15`
• 
  `r=0.04 \ rounded`