Question

Given the function f(x)=2x what is the correct transformed equation

Answer 1

The transformed equation:
`\(2 \cdot (x - 4)^2 + 2\)` represents a parabola shifted right, stretched vertically, and translated upward.

Starting with the function f(x) = x^2, we'll apply the given transformations: a vertical translation 2 units up, a stretch by a factor of 2, and a horizontal shift 4 units to the right.

1. Vertical Translation 2 Units Up: To shift the graph 2 units up, we modify the function by adding 2 to f(x): f(x) + 2.

2. Stretch by a Factor of 2: To stretch the graph vertically by a factor of 2, we multiply the function by 2:
`\(2 \cdot f(x)\)`.

3. Horizontal Shift 4 Units Right: To shift the graph 4 units right, we replace x in f(x) with x - 4) f(x - 4).

Combining these transformations, the order of operations is as follows:

1. Apply the horizontal shift: f(x - 4)

2. Stretch the function vertically:
`\(2 \cdot f(x - 4)\)`

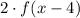
3. Apply the vertical translation:
`\(2 \cdot f(x - 4) + 2\)`

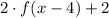
Therefore, the equation representing the combined transformations for
`\(f(x) = x^2\)` is
`\(2 \cdot (x - 4)^2 + 2\)`.

This equation represents a parabolic function that has been horizontally shifted 4 units to the right, stretched vertically by a factor of 2, and then translated 2 units up. This modified function will have its vertex at (4, 2) instead of the standard vertex at (0, 0), and it will open upwards, maintaining the shape of a parabola but with the described transformations applied.

Question:

Given the function f(x) =x^2, what is the equation that best represents the following transformations? Vertical translation 2 units up, stretch by a factor of 2, and a horizontal shift 4 units right.