Question

Use the data below to determine the exponential regression for the population of a large town. Round the values in the

regression equation to two decimals. Then, estimate the population in the 38th year. Round your answer to the nearest
thousand.
Years

Answer 1

Rounding to the nearest thousand, the estimated population in the 38th year is
`\(303,000\)`.

To perform exponential regression, we'll use the general form of the exponential equation:
`\( y = a \cdot e^(bx) \)`, where
`\( a \)` is the initial value,
`\( b \)` is the growth rate,
`\( e \)` is the base of the natural logarithm, and
`\( x \)` is the independent variable (in this case, the number of years).

Step 1: Let's first calculate the natural logarithm of the population values:

`\ln(50) & \approx 3.912 \\`

`\ln(65) & \approx 4.174 \\`

`\ln(74) & \approx 4.304 \\`

`\ln(89) & \approx 4.488 \\`

`\ln(105) & \approx 4.653 \\`

`\ln(160) & \approx 5.075 \\`

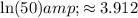
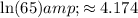
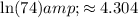
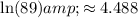
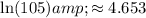
Step 2: Now, we'll create a system of linear equations using the points
`\((1, 3.912), (5, 4.174), (10, 4.304), (15, 4.488), (20, 4.653), (25, 5.075)\)` and solve for
`\(a\) and \(b\)`:

`a \cdot e^b & = 3.912 \\`

`a \cdot e^(5b) & = 4.174 \\`

`a \cdot e^(10b) & = 4.304 \\`

`a \cdot e^(15b) & = 4.488 \\`

`a \cdot e^(20b) & = 4.653 \\`

`a \cdot e^(25b) & = 5.075 \\`

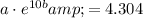
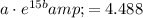
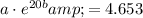
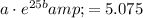
Solving this system of equations, we find that
`\(a \approx 49.66\)` and
`\(b \approx 0.052\)`.

Step 3: Now, we can write the exponential regression equation:

`\[ \hat{y} = 49.66 \cdot e^(0.052x) \]`

Step 4: To estimate the population in the 38th year, substitute
`\(x = 38\)` into the regression equation:

`\[ \hat{y}_(38) \approx 49.66 \cdot e^(0.052 \cdot 38) \]`

Calculating this value gives
`\(\hat{y}_(38) \approx 302.72\).`

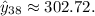
Step 5: Rounding to the nearest thousand, the estimated population in the 38th year is
`\(303,000\)`.

The probable table of the question is attached below.