Question

Please help me u also need to plot the points

Answer 1

The graph of the function shows a horizontal line at y = 1. This means that the function is a constant function with a value of 1. Therefore, coordinates of
`$P'$` under the transformation
`$T_(-4,0) \circ r_(m)$` is (-3,1).

The graph of the function shows a horizontal line at y = 1.

This means that the function is a constant function with a value of 1.

Therefore, for any input value x, the output value of the function will be 1.

The transformation
`$T_(-4,0)$` is a translation of 4 units to the left.

The transformation
`$r_(m)$` is a reflection across the line
`$y = mx$`.

To find the coordinates of
`$P'$` under the transformation
`$T_(-4,0) \circ r_(m)$`, we first reflect P across the line y =
`mx$`.

The line
`$y = mx$` passes through the point P, so
`$m = 1$`.

Therefore, the reflection of P across the line
`$y = mx$` is the point P' at
`$(1,1)$`

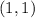
Next, we translate
`$P'$` 4 units to the left.

This gives us the coordinates of P' under the transformation
`$T_(-4,0) \circ r_(m)$`, which is
`$(-3,1)$`.

Here is a more detailed explanation of each step:

1. **Reflection across the line
`$y = mx$`:**

To reflect a point
`$(a,b)$` across the line
`$y = mx$`, we first find the equation of the perpendicular line that passes through
`$(a,b)$`.

The slope of the perpendicular line is
`$-(1)/(m)$`, so the equation of the perpendicular line that passes through
`$(a,b)$` is
`$y = -(1)/(m)x + b$`.

We then find the point of intersection of the perpendicular line and the line y = mx.

The x-coordinate of the point of intersection is the solution to the equation
`$-(1)/(m)x + b = mx$`.

Solving for x, we get
`$x = (bm)/(m^2 + 1)$`.

The y-coordinate of the point of intersection is then found by substituting
`$x = (bm)/(m^2 + 1)$` into the equation y =
`v`.

This gives us
`$y = (bm^2)/(m^2 + 1)$`.

Therefore, the reflection of the point
`$(a,b)$` across the line
`$y = mx$` is the point
`$\left( (bm)/(m^2 + 1), (bm^2)/(m^2 + 1) \right)$`.

2. Translation:

To translate a point
`$(a,b)$` by
`$(h,k)$`, we simply add
`$h$` to the x-coordinate and
`$k$` to the y-coordinate. This gives us the coordinates of the translated point, which is
`$(a + h, b + k)$`.

Therefore, to translate the point
`$(a,b)$` by
`$(-4,0)$`, we add
`$-4$` to the x-coordinate and 0 to the y-coordinate. This gives us the coordinates of the translated point, which is (a - 4, b).

Conclusion:

The coordinates of
`$P'$` under the transformation
`$T_(-4,0) \circ r_(m)$` is (-3,1).