The derivative of
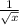 with respect to
with respect to
 is
is
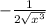 .
.
How did we get the value?
To find the derivative of
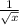 , you can use the rules of differentiation.
, you can use the rules of differentiation.
Let \( y =
 . To find
. To find
 :
:
![\[ y = x^(-1/2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/g2ifatracmnf3ncsaxh5798c47dbilbxdw.png)
Now, apply the power rule for differentiation, which states that if
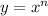 , then
, then
 :
:
![\[ (dy)/(dx) = -(1)/(2)x^(-3/2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/kr279x8n9a3nyttli5mfv5n6aw5e0zcff5.png)
Now, you can simplify the expression:
![\[ (dy)/(dx) = -(1)/(2√(x^3)) \]](https://img.qammunity.org/2024/formulas/mathematics/college/ljyi8g4m8ghefl2iq00n4w4bfvrlh7piea.png)
So, the derivative of
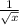 with respect to
with respect to
 is
is
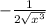 .
.