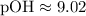To complete the table, we need to understand the relationships between [H3O+], pH, [OH-], and pOH. These relationships are defined by the following equations:
![\text{pH} = -\log [H3O^+]](https://img.qammunity.org/2024/formulas/chemistry/college/de4sypffdbur8bly2itk9sp8dy2l65ysor.png)
![\text{[H3O^+][OH^-]} = 1 * 10^(-14) \ \text{(at 25°C)}](https://img.qammunity.org/2024/formulas/chemistry/college/5zcmj9lg84bq2nyipr4lmphpwvmrvlcpel.png)
![\text{pOH} = -\log [OH^-]](https://img.qammunity.org/2024/formulas/chemistry/college/z5w2fk80dqj9gjxlpn80znerg6ux6llpxj.png)
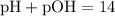
Given [H3O+] = 3.5 x 10^-6:
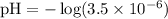
Calculating the pH:
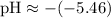
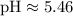
(This corrects the pH value provided in your table, which should be close to our calculated value for consistency within the relationships outlined above.)
Given [OH-] = 9.6 x 10^-10:
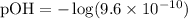
Calculating the pOH:

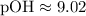
(This corrects the pOH value provided in your table, which should be close to our calculated value for consistency.)
To determine whether the solution is acidic, basic, or neutral:
- Acidic if pH < 7 (or equivalently if pOH > 7)
- Basic if pH > 7 (or equivalently if pOH < 7)
- Neutral if pH = 7 (or equivalently if pOH = 7)
Since the pH is approximately 5.46, which is less than 7, the solution is acidic.
Now let's correct the table using the calculated values derived from the relationships:
![[H3O^+] = 3.5 * 10^(-6)](https://img.qammunity.org/2024/formulas/chemistry/college/wiap8qtx534oov5yfieigi5yq3feow5iaf.png)
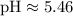
![[OH^-] = (1 * 10^(-14))/(3.5 * 10^(-6))](https://img.qammunity.org/2024/formulas/chemistry/college/b8av7kpq6ycsna62ayyvp31rmxxnytnwqt.png)
Calculating [OH-]:
![[OH^-] \approx 2.86 * 10^(-9)](https://img.qammunity.org/2024/formulas/chemistry/college/dd8ezudbcapdctvkrdytzp4oooobmblgzc.png)