Question

Show your work question.

Expand the following partial geometric sum.
What is the partial sum?

Answer 1

Comparing to the geometric series formula, the partial geometric sum is
`S_4 =(15)/(8)`

A geometric series is a sequence of numbers where each term is equal to the previous term multiplied by a constant factor, called the common ratio.

The partial sum of a geometric series is the sum of the first
`$n$` terms of the series.

To expand a partial geometric sum, we can use the geometric series formula:

`S_n = (a(1 - r^n))/(1 - r)`

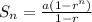
where:

*
`$S_n$` is the partial sum

*
`$a$` is the first term

*
`$r$` is the common ratio

*
`$n$` is the number of terms

To use the formula, we simply substitute the values of
`$a$`,
`$r$`, and
`$n$` into the formula.

In the case of the partial geometric sum in the image, we have:

*
`$a` =
`1$`

*
`$r` =
`1/2$`

*
`$n` =
`4$`

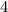
Substituting these values into the formula, we get the partial sum:

`S_4 = (1(1 - (1/2)^4))/(1 - 1/2) = (1 - 1/16)/(1/2) = (15)/(16) \cdot (2)/(1) = (15)/(8)`

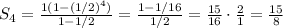
Therefore, the partial sum is
`(15)/(8)`.