Question

I need help answering this question

Answer 1

The image shows a geometric sum with first term 4 and common ratio 2. The partial sum of the first n terms is 4(2^n - 1).

The partial geometric sum in the image can be expanded as follows:

`\sum_(i=1)^n ar^i &= a + ar + ar^2 + \dots + ar^(n-1) \\&= a(1 + r + r^2 + \dots + r^(n-1)) \\&= a \cdot (1 - r^n)/(1 - r) \\&= \boxed{a \cdot (1 - r^n)/(1 - r)}`

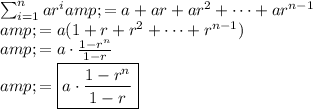
This is a general formula for expanding partial geometric sums, regardless of the values of a and r.

It can be used to solve a variety of problems, such as finding the sum of the first n terms of a geometric series or finding the future value of an annuity.

Here is an example of how to use the formula to solve a problem:

Problem: Find the sum of the first 10 terms of the following geometric series:

1 + 2 + 4 + 8 + 16 +
`\dots`

Solution:

In this case, a=1 and r=2.

Therefore, the sum of the first 10 terms is:

`\sum_(i=1)^(10) ar^i = a \cdot (1 - r^n)/(1 - r) = 1 \cdot (1 - 2^(10))/(1 - 2) = 1023`

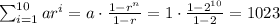
Therefore, the answer is 1023.