The simplified expression is
![\frac{150 √(5) }{4√(15)-4\sqrt[4]{10} }](https://img.qammunity.org/2024/formulas/mathematics/high-school/8okahkg3h99qu4xxv90p8wnvehllupoe61.png) .
.
Simplify the numerator:
 : Use the power of a power rule:
: Use the power of a power rule:
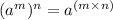
This gives us
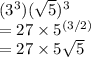
 : Use the constant multiple rule:
: Use the constant multiple rule:
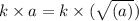
This gives us
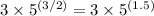
Combine the terms in the numerator:
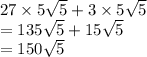
Simplify the denominator:
- Factor the radicals in both terms:
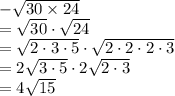
![& -\sqrt[4]{25 * 16}\\=\sqrt[4]{25} \cdot \sqrt[4]{16}\\=\sqrt[4]{5 \cdot 5} \cdot \sqrt[4]{2 \cdot 2 \cdot 2 \cdot 2}\\=2 \sqrt[4]{5} \cdot 2 \sqrt[4]{2}\\=4 \sqrt[4]{10}](https://img.qammunity.org/2024/formulas/mathematics/high-school/8l56jg7tzgbrzilumucqtq4y7c6hk36ci0.png)
Substitute the simplified numerator and denominator into the fraction:
![\frac{150 √(5) }{4√(15)-4\sqrt[4]{10} }](https://img.qammunity.org/2024/formulas/mathematics/high-school/8okahkg3h99qu4xxv90p8wnvehllupoe61.png)