Question

Please help, need answer quickly!!! thank youuuuu

Answer 1

The value of angle QRS is 41°.

The strategy is to use the fact that the exterior angle of a triangle is equal to the sum of the two interior opposite angles.

In the triangle formed by the points P, Q, and R, ∠QRS is an exterior angle. The two interior opposite angles are ∠ PQR and ∠RPQ.

Using the given information, we know that:

-
`$m \angle P Q R=(x+18)^(\circ)$`

-
`$m \angle Q R S=(6 x-13)^(\circ)$`

-
`$m \angle R P Q=(2 x-4)^(\circ)$`

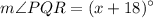
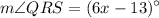
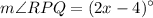
We can now set up an equation to relate these angles:

`m \angle Q R S=m \angle P Q R+m \angle R P Q`

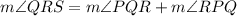
Substituting the values we know:

(6x - 13)° = (x+18)° + (2x-4)°

6x -x -2x = 18 - 4 +13

6x - 3x = 18 + 9

3x = 27

Dividing both sides by 3 we get

x = 9

To find the value of ∠QRS put the value of x in the given value.

∠QRS = (6 x-13)°

∠QRS = 6 x 9 - 13

∠QRS = 54 -13

∠QRS = 41°