Question

Given the graph of the logarithmic function below, determine the equation in the form f(x) = logb (x-h).

Answer 1

The equation of the graph in the form f(x) =
`\log_b(x - h)` is; f(x) = log₂(x + 3)

The steps used to find the equation of the graph is presented as follows;

The asymptote of the graph of the logarithmic function is; x = -3

Therefore, the graph is shifted 3 units to the right, which indicates that the value of h in the function f(x) =
`\log_b(x-h)` is; h = -3, from which we get;

f(x) =
`\log_b(x-(-3))`

`\log_b(x-(-3))` =
`\log_b(x+3)`

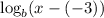
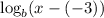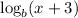
f(x) =
`\log_b(x+3)`

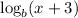
The coordinate points on the graph includes; (-2, 0), (-1, 1), and (5, 3)

Plugging in the values, we get;

f(-1) = 1

f(-1) =
`\log_b(-1+3)`

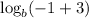
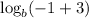`\log_b(-1+3)` = 1

b¹ = 2

b = 2

The logarithmic function is therefore; f(x) = log₂(x + 3)