Answer:
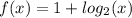
Explanation:
The given function is
 , and we know some points such that f passes through them, like (1,1) and (2,2). then we can get the next equations:
, and we know some points such that f passes through them, like (1,1) and (2,2). then we can get the next equations:
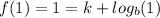
but
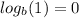 given that
given that
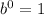 for any number b, then:
for any number b, then:
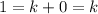
Similar, we can take the point (2,2):
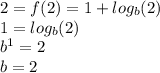
The last equalities are given by definition of logarithm