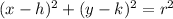Question

What is the equation of this circle in standard form? Diagram shows a circle with diameter MN. The coordinates of M are (2, 4) and the coordinates of N are (9, 4).

Answer 1

Answer:
`(x-(11)/(2))^2+(y-4)^2=(49)/(4)`

Explanation:

We need to find the center and the radius of the circle. As we have the terminal points of a diameter (M and N) then the center (h,k) is the middle point of segment MN, then:

`h=(2+9)/(2)=(11)/(2)\\k=(4+4)/(2)=(8)/(2)=4`

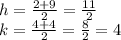
Finally, the radius r is half of the size of MN, then:

`r=(1)/(2)√((9-2)^2+(4-4)^2)=(7)/(2)\\`

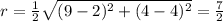
Now, the equation of a circumference has the next form:

`(x-h)^2+(y-k)^2=r^2`