Question

In the diagram, line and line are horizontal lines and is a vertical line segment. If FB : FC = 4 : 3, what are the coordinates of point D? Two horizontal bidirectional arrows in parallel have a triangle with points A equals (negative 10, negative 8) and B at the bottom arrow and C equals (negative 3, negative 1) on the right top away from the top arrow, E D F are at the top arrow. A. (-4, -2) B. (-5, -3) C. (-6, -4) D. (-7, -5) E. (-8, -6)

Answer 1

The coordinates of the point D that divides the segment AC in the ratio 4 : 3 are (-6, -4). The correct option is therefore;

C. (-6, -4)

The steps used to find the coordinates of the point D are as follows;

The lines
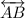`\overleftrightarrow{AB}` and
`\overleftrightarrow{EF}` are parallel lines. Whereby FB : FC = 4 : 3, we get;

AD : DC = 4 : 3

The section formula indicates that the coordinates, (x, y), of a point that divides a segment (x₁, y₁), (x₂, y₂) in the ratio m : n are;

`[(m\cdot x_2 + n\cdot x_1)/(m + n), (m\cdot y_2 + n\cdot y_1)/(m + n)]`

Therefore, the coordinates of the point D that divides AC in the ratio 4 : 3 are;

`[(4* (-3) + 3* (-10))/(4 + 3), (4* (-1) + 3* (-8))/(4 + 3)] = (-6, -4)`

The coordinates of the point D are (-6, -4)

The complete question obtained from a similar question found through search is presented as follows;

In the diagram
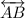`\overleftrightarrow{AB}` and
`\overleftrightarrow{EF}` are horizontal lines and
`\overline{CB}` is a vertical line segment. If FB : FC = 4 : 3, what are the coordinates of point D.

Please find attached, the possible drawing of the diagram, created with MS Word