Question

In a geometric sequence the second term is - 6 and the Seventh term is - 1458 find its 5th term​

Answer 1

`\sf a_5 = -162`

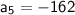
Explanation:

In a geometric sequence, each term is obtained by multiplying the previous term by a constant called the common ratio (
`\sf r`). Let's denote the first term as
`\sf a` and the common ratio as
`\sf r`.

The general formula for the
`\sf n`-th term (
`\sf a_n`) in a geometric sequence is given by:

`\sf a_n = a \cdot r^((n-1))`

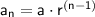
Given that the second term (
`\sf a_2`) is -6, and the seventh term (
`\sf a_7`) is -1458, we can use these values to set up equations:

1. For the second term:

`\sf a_2 = a \cdot r^((2-1)) = -6`

`\sf a \cdot r = -6`

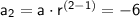
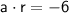
2. For the seventh term:

`\sf a_7 = a \cdot r^((7-1)) = -1458`

`\sf a \cdot r^6 = -1458`

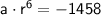
Now, we can use the first equation to express
`\sf a` in terms of
`\sf r`:

`\sf a = -(6)/(r)`

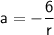
Substitute this expression for
`\sf a` into the second equation:

`\sf -(6)/(r) \cdot r^6 = -1458`

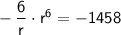
Simplify the equation:

`\sf -6 \cdot r^5 = -1458`

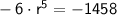
Divide both sides by -6:

`\sf (-6 \cdot r^5)/(-6) = (-1458)/(-6)`

`\sf r^5 = 243`

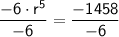
Now, take the fifth root of both sides to solve for
`\sf r`:

`\sf r = \sqrt[5]{243}`

`\sf r = ३`

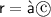
Now that we know the common ratio (
`\sf r = 3`), we can find the first term (
`\sf a`) using the first equation:

`\sf a \cdot 3 = -6`

`\sf a = -2`

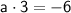
Finally, we can find the fifth term (
`\sf a_5`):

`\sf a_5 = -2 \cdot 3^((5-1))`

`\sf a_5 = -2 \cdot 3^4`

`\sf a_5 = -2 \cdot 81`

`\sf a_5 = -162`

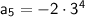
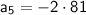
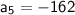
Therefore, the fifth term of the geometric sequence is -162.