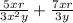Question

(5xr)/(3x^(2)y)+(7xr)/(3y)

Answer 1

The simplified form of the expression is
`(5 x r)/(3 x^2 y)+(7 x r)/(3 y)=(5 x r y+7 x^2 r)/(3 x^2 y)`

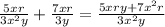
To simplify the expression
`$(5 x r)/(3 x^2 y)+(7 x r)/(3 y)$`, let's find a common denominator and combine the fractions.

Factor out the common terms from both denominators.

5 x r has a denominator of
`$3 x^2 y$` and 7xr has a denominator of 3y.

Find the least common denominator (LCD) for
`$3 x^2 y$` and
`$3 y$`.

The LCD is
`$3 x^2 y$` as it encompasses both denominators.

Rewrite the fractions with the LCD.

`& (5 x r)/(3 x^2 y)=(5 x r \cdot y)/(3 x^2 y \cdot y)=(5 x r y)/(3 x^2 y^2) \\& (7 x r)/(3 y)=(7 x r \cdot x)/(3 y \cdot x)=(7 x^2 r)/(3 x^2 y)`

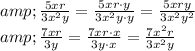
Combine the fractions with the common denominator.

`(5 x r y)/(3 x^2 y^2)+(7 x^2 r)/(3 x^2 y)=(5 x r y+7 x^2 r)/(3 x^2 y)`

Question:

Simplify
`\((5xr)/(3x^2y) + (7xr)/(3y)\)`