Question

An airline company is interested in improving customer satisfaction rate from the 61% currently claimed. The company sponsored a survey of 292 customers and found that 192 customers were satisfied. Determine whether sufficient evidence exists that the customer satisfaction rate is higher than the claim by the company.

What is the test statistic z?
What is the p-value?
Does sufficient evidence exist that the customer satisfaction rate is different than the claim by the company at a significance level of 0.1?

Answer 1

The calculated test statistic z is approximately 1.83.

The p-value is approximately 0.0336.

There is sufficient evidence to suggest that the customer satisfaction rate is higher than the claimed 61% at a significance level of 0.1.

How to determine whether there is sufficient evidence

To determine whether there is sufficient evidence that the customer satisfaction rate is higher than the claimed 61%, perform a hypothesis test.

Null Hypothesis (H0): The customer satisfaction rate is equal to or lower than 61%.

Alternative Hypothesis (Ha): The customer satisfaction rate is higher than 61%.

Given:

Sample size (n) = 292

Number of satisfied customers (x) = 192

Claimed customer satisfaction rate (p) = 61%

To test the hypothesis, calculate the test statistic z and the corresponding p-value.

The test statistic z can be calculated using the formula:

`z = (x - np) / \sqrt(np(1-p))`

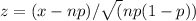
Where:

x = Number of satisfied customers

n = Sample size

p = Claimed customer satisfaction rate

Substitute the values into the formula:

z = (192 - 292 * 0.61) /
`\sqrt`(292 * 0.61 * (1-0.61))

z ≈ 1.83

The calculated test statistic z is approximately 1.83.

To find the p-value, use a standard normal distribution table or a statistical software.

From the z-value, determine the area under the standard normal curve to the right of z.

The p-value is the probability of observing a test statistic as extreme as (or more extreme than) the calculated value.

Using a standard normal distribution table or statistical software, the p-value for a z-value of 1.83 is approximately 0.0336.

At a significance level of 0.1 (or 10%), if the p-value is less than the significance level, we reject the null hypothesis. In this case, the p-value (0.0336) is less than 0.1, so we can reject the null hypothesis.

Therefore, there is sufficient evidence to suggest that the customer satisfaction rate is higher than the claimed 61% at a significance level of 0.1.