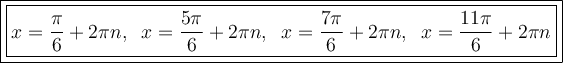Question

4cos^2(x) + csc^2(x) - 7 = 0

Can you show me how to solve this exercise?​

Answer 1

`x=(\pi)/(6)+2\pi n, \;\;x=(5\pi)/(6)+2\pi n, \;\;x=(7\pi)/(6)+2\pi n, \;\;x=(11\pi)/(6)+2\pi n`

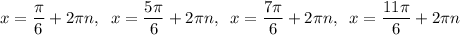
Explanation:

Given trigonometric equation:

`4\cos^2x+\csc^2x-7=0`

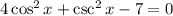
To solve the equation for x, begin by rewriting csc²x using the reciprocal identity:

`4\cos^2x+(1)/(\sin^2x)-7=0`

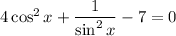
Now, rewrite cos²x in terms of sin²x by using the Pythagorean identity sin²x + cos²x = 1:

`4(1-\sin^2x)+(1)/(\sin^2x)-7=0`

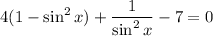
Expand:

`4-4\sin^2x+(1)/(\sin^2x)-7=0`

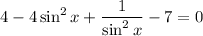
Simplify:

`-4\sin^2x+(1)/(\sin^2x)-3=0`

`4\sin^2x-(1)/(\sin^2x)+3=0`

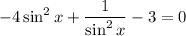
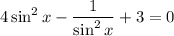
Multiply every term by sin²x to clear the fraction:

`4\sin^4x-1+3\sin^2x=0`

`4\sin^4x+3\sin^2x-1=0`

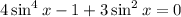
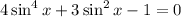
Now, let u = sin²x:

`4u^2+3u-1=0`

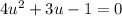
Factor the quadratic:

`\begin{aligned}4u^2+3u-1&=0\\4u^2+4u-u-1&=0\\4u(u+1)-1(u+1)&=0\\(4u-1)(u+1)&=0\end{aligned}`

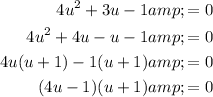
Solve for u:

`\begin{aligned}4u-1&=0 \implies u=(1)/(4)\\\\u+1&=0 \implies u=-1\end{aligned}`

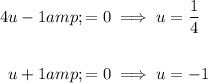
Substitute back in u = sin²x, and solve each equation for x.

`\sin^2x=(1)/(4) \implies \sin x=\pm (1)/(2)`

`x=\sin^(-1)\left(-(1)/(2)\right)\implies x=(7\pi)/(6)+2\pi n, (11\pi)/(6)+2\pi n`

`x=\sin^(-1)\left((1)/(2)\right)\implies x=(\pi)/(6)+2\pi n, (5\pi)/(6)+2\pi n`

`\sin^2x=-1 \implies \sf unde\:\!fined`

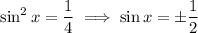
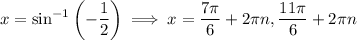
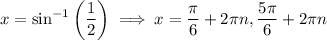
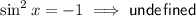
Therefore, the solutions to the given trigonometric equation are:

`\large\boxed{\boxed{x=(\pi)/(6)+2\pi n, \;\;x=(5\pi)/(6)+2\pi n, \;\;x=(7\pi)/(6)+2\pi n, \;\;x=(11\pi)/(6)+2\pi n}}`